
 Figura 1. Dirección de los cambios de entropía en el enfriamiento de un cuerpo.
Figura 1. Dirección de los cambios de entropía en el enfriamiento de un cuerpo. Figura 2: Ludwig Boltzmann (1844-1906)
Figura 2: Ludwig Boltzmann (1844-1906)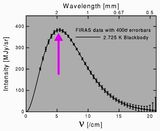 Figura 3. Espectro del fondo cósmico de radiación. Ejemplo casi perfecto de la radiación de un cuerpo negro, esto es, de un sistema en equilibrio termodinámico.
Figura 3. Espectro del fondo cósmico de radiación. Ejemplo casi perfecto de la radiación de un cuerpo negro, esto es, de un sistema en equilibrio termodinámico. Figura 4. Esquema de la evolución del universo, con sus principales etapas indicadas: recombinación (y origen de la radiación de fondo), etapa oscura, formación de las primeras estrellas, las primeras galaxias, hasta la etapa actual con la existencia de cúmulos de galaxias.
Figura 4. Esquema de la evolución del universo, con sus principales etapas indicadas: recombinación (y origen de la radiación de fondo), etapa oscura, formación de las primeras estrellas, las primeras galaxias, hasta la etapa actual con la existencia de cúmulos de galaxias. Figura 5. El físico austríaco Erwin Schrödinger (1887-1961)
Figura 5. El físico austríaco Erwin Schrödinger (1887-1961) Figura 6. La tierra absorbe fotones de alta energía del sol, y los re-emite como un número mayor de fotones de más baja energía, conservando la energía total pero disminuyendo la entropía local.
Figura 6. La tierra absorbe fotones de alta energía del sol, y los re-emite como un número mayor de fotones de más baja energía, conservando la energía total pero disminuyendo la entropía local. Figura 7. Henri Poincaré (1854-1912)
Figura 7. Henri Poincaré (1854-1912)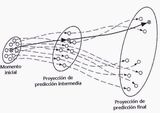 Figura 8. Sistema caótico. Pequeñas variaciones en las condiciones iniciales se manifiestan como grandes desviaciones en las trayectorias resultantes.
Figura 8. Sistema caótico. Pequeñas variaciones en las condiciones iniciales se manifiestan como grandes desviaciones en las trayectorias resultantes. Figura 9. Ilya Prigogine (1917-2003)
Figura 9. Ilya Prigogine (1917-2003) "La Segunda Ley de la Termodinámica nunca podrá ser probada matemáticamente por medio de las ecuaciones de la dinámica solamente."
"La Segunda Ley de la Termodinámica nunca podrá ser probada matemáticamente por medio de las ecuaciones de la dinámica solamente."Ludwig Boltzmann
 Dr. Gustavo E. Romero
Dr. Gustavo E. RomeroIrreversibilidad, caos y tiempo
Un hecho notable del mundo es que cambia. La existencia del cambio fue un gran problema para la filosofía griega anterior a Sócrates. Parménides de Elea, famosamente, escribió que lo que es, es, y lo que no es, no es. Por tanto, señaló, lo que es no puede surgir de lo que no es. De ello infirió que el cambio es imposible, ya que cambiar es dejar de ser algo en algún aspecto para ser otra cosa. Negó también el movimiento, ya que moverse, entendió, es ocupar un lugar que antes estaba vacío. Como el vacío es lo que no es, no puede existir, y por tanto no puede haber movimiento. Zenón, también de Elea y discípulo de Parménides, desarrolló paradojas que tratan de mostrar que el movimiento, y por tanto el cambio, no son posibles. Por ejemplo, Aquiles decide recorrer una cierta distancia, digamos de A hasta B. Llamemos a esa distancia AB. Para recorrer AB debe recorrer primero AB/2, y antes la mitad de eso, AB/4, y antes la mitad, y así hasta el infinito. O sea que debe realizar infinitos recorridos, todos ellos finitos, en un tiempo finito. Según Zenón, esto es absurdo. Luego, la hipótesis debe ser falsa: Aquiles no puede moverse.
Hay muchas paradojas que involucran el movimiento, la divisibilidad, y el infinito, como las paradojas de Zenón. Sin duda, estas paradojas han sido un gran estímulo para el pensamiento. Podría incluso decirse que toda la metafísica occidental y buena parte de las matemáticas han derivado de intentos de solucionar o resolver estas paradojas.
El cambio fue aceptado como componente esencial del mundo a partir de las respuestas al desafío Eleático formuladas por los atomistas y por Aristóteles. Los atomistas, Leucipo y Demócrito, ambos de Abdera, primero, y mucho después Epicuro y sus discípulos, presentaron una teoría del cambio que parte de 1) la existencia del vacío, y 2) la existencia de elementos indivisibles (átomos). Toda cosa está compuesta de átomos. Hay diferentes tipos de átomos y diferentes formas de combinarlos. Un cambio en una cosa no es más que un cambio en la estructura atómica subyacente.
Aristóteles, por su parte, expresó su opinión de que las cosas son sustancias con propiedades. El cambio es permanencia de sustancia con modificación de las propiedades. El cambio, pues, puede suceder sin movimiento y sin destrucción de la sustancia: puede ocurrir sin necesidad de que algo salga de la nada.
La idea aristotélica predominó hasta el renacimiento, cuando la concepción atómica volvió a ser valorada. Con el advenimiento de la ciencia moderna y el desarrollo del cálculo diferencial e integral, pareció que por primera vez una descripción cuantitativa del cambio era posible. Galileo, Newton y Leibniz, entre otros, desempeñaron un papel importante en estos avances. Sin embargo, es recién en el Siglo XIX que se desarrollan los fundamentos rigurosos del análisis matemático, por parte de Weierstrass, Dedekind y Cantor, entre otros. En ese mismo siglo la teoría mecánica de Newton es llevada a su máximo desarrollo, incorporándose la teoría de campos continuos y la termodinámica.
La termodinámica fue desarrollada a partir de los trabajos pioneros de Sadi Carnot, considerado el "padre de termodinámica". En 1824 publicó Reflexiones sobre la Energía Motriz del Fuego, un discurso sobre la eficiencia térmica, la energía, la energía motriz y el motor. El documento describe las relaciones básicas energéticas entre la máquina de Carnot, el ciclo de Carnot y la energía motriz, marcando el inicio de la termodinámica como ciencia moderna.
El primer libro de texto sobre termodinámica fue escrito en 1859 por William Rankine, que originalmente se formó como un físico y profesor de ingeniería civil y mecánica en la Universidad de Glasgow. La primera y la segunda ley de la termodinámica surgieron simultáneamente en la década de 1850, principalmente por la obras de Germain Henri Hess, William Rankine, Rudolf Clausius, James Prescott Joule y William Thomson (Lord Kelvin).
Los fundamentos de la termodinámica estadística se establecieron por los físicos como James Clerk Maxwell, Ludwig Boltzmann, Max Planck, Rudolf Clausius, Johannes van der Waals y J. Willard Gibbs. En particular, la segunda ley de la termodinámica (la primera expresa básicamente la conservación de la energía) puede parafrasearse diciendo que no es posible ningún proceso cuyo único resultado sea la extracción de calor de un recipiente a una cierta temperatura y la absorción de una cantidad igual de calor por un recipiente a temperatura más elevada. En otras palabras, los procesos en el mundo real son irreversibles. Es posible formular la segunda ley en términos de la llamada entropía de un sistema físico.
La entropía física S, en su forma clásica, está definida por la ecuación siguiente:
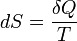
donde Q representa el calor o trabajo realizado sobre el sistema y T su temperatura. Esto es equivalente a la siguiente relación:
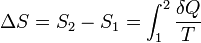
o, más simplemente, cuando no se produce variación de temperatura (proceso isotérmico):
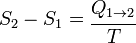
donde 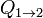 es la cantidad de calor intercambiada entre el sistema y el entorno, y T es la temperatura absoluta en Kelvin. Los números 1 y 2 se refieren a los estados iniciales y finales del sistema termodinámico.
es la cantidad de calor intercambiada entre el sistema y el entorno, y T es la temperatura absoluta en Kelvin. Los números 1 y 2 se refieren a los estados iniciales y finales del sistema termodinámico.
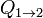 es la cantidad de calor intercambiada entre el sistema y el entorno, y T es la temperatura absoluta en Kelvin. Los números 1 y 2 se refieren a los estados iniciales y finales del sistema termodinámico.
es la cantidad de calor intercambiada entre el sistema y el entorno, y T es la temperatura absoluta en Kelvin. Los números 1 y 2 se refieren a los estados iniciales y finales del sistema termodinámico.Cuando un sistema termodinámico pasa, en un proceso reversible e isotérmico, del estado 1 al estado 2, el cambio en su entropía es igual a la cantidad de calor intercambiado entre el sistema y el medio, dividido por su temperatura absoluta.
El físico austríaco Ludwig Boltzmann desarrolló en la segunda mitad del siglo XIX lo que hoy se conoce como mecánica estadística, teoría profundamente influenciada por el concepto de entropía. Una de las teorías termodinámicas estadísticas (la teoría de Maxwell-Boltzmann) establece la siguiente relación entre la entropía y la cantidad de micro-estados de las componentes (moleculares o atómicas) de un sistema termodinámico en el equilibrio:
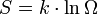
donde k es la constante de Boltzmann y Ω el número de micro-estados posibles para el sistema (ln es la función logaritmo neperiano). La ecuación anterior es válida porque se supone que todos los micro-estados tienen la misma probabilidad de aparecer (situación de equilibrio). En términos de la entropía, la segunda ley de la termodinámica puede expresarse como:
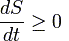
O sea, la cantidad de entropía del universo tiende a incrementarse con el tiempo. La segunda ley expresa, si hemos de decirlo en palabras simples, que todo se degrada. En el estado de equilibrio termodinámico, la entropía alcanza un valor máximo. En el equilibrio, la temperatura de un sistema es igual a la del medio, y ya no hay flujos de calor. La entropía ya no cambia. Para un sistema biológico, morir es, pues, llegar al equilibrio termodinámico: el estado de máximo desorden, el estado en el cual ya no se puede hacer trabajo. Ese estado en el cual nuestro cuerpo está a la misma temperatura que el lugar donde es depositado. (Fig.1)
Una noche de 1997, recuerdo haberle dicho a Héctor Vucetich, en un apartamento de São Paulo de la rua Frei Caneca, que la segunda ley de la termodinámica es la formulación matemática del sentimiento trágico de la vida. Aún lo pienso, confirmado por los años y lo que ellos traen.
¿Cuál es la razón de la irreversibilidad proclamada por la segunda ley? Acaso no haya ley más corroborada por la experiencia que ésta. Pero...¿porqué el mundo es así? ¿porqué debemos, inexorablemente, envejecer y morir? Puede parecer natural, pero eso es sólo un efecto de la costumbre.
Basta que algo extraordinario se repita unas cuantas veces y nos parece obvio. La mera costumbre puede llevarnos a aceptar como evidentes las cosas más asombrosas. Pensemos un momento: todas las leyes básicas de la física son reversibles bajo inversión temporal. Esto significa que ellas no distinguen pasado de futuro.
Si reemplazamos el tiempo (t) por su opuesto (-t) en las ecuaciones que representan las leyes de la mecánica, del electromagnetismo, de la gravitación, de la mecánica cuántica, de la teoría de campos, siempre, siempre obtenemos las mismas soluciones. ¿Porqué, entonces, la entropía crece? ¿Porqué el pasado es diferente del futuro? ¿Porqué siempre envejecemos, y nunca nos volvemos más jóvenes? Ludwig Boltzmann creyó encontrar la respuesta a estas preguntas.
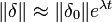
- El origen de la irreversibilidad
Ludwig Boltzmann nació el 20 de febrero de 1844 en Viena y dedicó su vida a formular los fundamentos microscópicos de la termodinámica. Boltzmann logró mostrar que una cierta función de las propiedades microscópicas de un sistema físico, que él llamó H, adquiere un valor extremo en el estado de equilibrio termodinámico. La inversa de esta función fue identificada con la entropía termodinámica, que es máxima en el equilibrio. Boltzmann afirmó que la razón por la cual la entropía crece en sistemas fuera del equilibrio no está en las ecuaciones sino en las condiciones iniciales de esas ecuaciones. Boltzmann fue el primero en formular claramente lo que hoy se conoce como Hipótesis del Pasado: "La fase actual del universo tuvo su origen en un estado de muy baja entropía, esto es, de gran orden". (Fig.2)
Boltzmann pensó que ese estado de orden era el fruto de una mera fluctuación estadística de los valores medios de la entropía. Hoy sabemos, sin embargo, que la probabilidad de una fluctuación tan grande como para dar lugar a todo el universo observable es prácticamente cero. De hecho, es inmensamente más probable que Ud., el lector, haya aparecido como una mera fluctuación de un "caldo" de partículas en equilibrio un instante atrás con todos sus recuerdos ya formados en su cerebro, que el universo lo haya hecho hace miles de millones de años y haya evolucionado hasta arrojar el mismo resultado.
Sea lo que haya pasado hace unos 13700 millones de años, cuando la fase de expansión actual del universo se originó, debe haber sido algo tal que la entropía global era muy, muy baja. Esto plantea un problema, ya que observaciones del universo primitivo muestran que en éste la materia y la radiación estaban en un estado de casi perfecto equilibrio, esto es, de máxima entropía. En efecto, las medidas de la distribución de la radiación cósmica de fondo realizadas por satélites como COBE, WMAP, y Planck, revelan el espectro de cuerpo negro más perfecto jamás detectado, claramente señalando un estado de equilibrio. En el equilibro la entropía es máxima. ¿Cómo puede ser entonces esto compatible con la Hipótesis del Pasado?
Roger Penrose, un físico-matemático de Oxford, ha propuesto una solución a esta aparente paradoja. El orden y la baja entropía en el universo temprano, señala Penrose, están asociados no a la materia y la radiación, sino al campo gravitacional. El estado natural de equilibrio del campo gravitacional es el colapso total. La gravedad es una fuerza atractiva; cuanto más compactos sean los sistemas gravitantes, más cerca del equilibrio estará el campo gravitacional. El estado de máximo equilibrio es lo que llamamos un agujero negro, un objeto completamente colapsado bajo su propio peso, hasta el punto que en su hundimiento ha arrastrado al propio espacio-tiempo. Pues bien, al comienzo del universo, o al menos de su fase actual, no había agujeros negros. No había estructura alguna. La materia y la radiación estaban homogéneamente distribuidas, en equilibrio entre ellas, pero muy lejos del equilibrio gravitacional. Con el paso del tiempo, pequeñas in-homogeneidades de origen cuántico fueron creciendo, dando lugar a estructuras más complejas, primero a estrellas gigantes llamadas estrellas de población III, y luego a galaxias, agujeros negros, más estrellas, planetas, Ud., y yo. Todo a costa de la baja entropía inicial del campo gravitacional. (Fig.4)
La irreversibilidad, según esta visión, tuvo su origen en la inusual situación del campo gravitacional hace casi 14000 millones de años. ¿Por qué el campo gravitacional fue tan homogéneo, tan desprovisto de estructura, en esa época? El responder esta pregunta es, quizás, el mayor desafío de la cosmología. Como el universo en esa época tenía el tamaño de una partícula sub-atómica, es de esperar que los efectos cuánticos en la gravedad hayan sido importantes. Nadie, por desgracia, ha podido construir aún una teoría cuántica de la gravedad que sea satisfactoria. Al menos, sabemos que debe predecir dicha teoría para el comienzo del universo: un estado de muy baja entropía.
- Sistemas biológicos y entropía
Los sistemas biológicos son sorprendentes en muchos aspectos. En particular, parecen violar la segunda ley de la termodinámica. Son sistemas altamente ordenados que se mantienen fuera del equilibrio respecto a su entorno. El que sean particularmente estables y ordenados muestra, sin embargo, que se comportan, como todo sistema, según las leyes de la física. Siguiendo al físico austríaco Erwin Schrödinger podríamos decir que la vida es un estado de la materia ordenado y sujeto a leyes con procesos que se oponen a la tendencia general de ir del orden al desorden, de la baja a la alta entropía. De hecho, cuando un sistema biológico llega al equilibrio termodinámico con el medio, decimos que ha muerto, y dejamos de considerarlo como un ser viviente.
Schrödinger sugirió, en los años 1940, que los sistemas biológicos tienen la capacidad de "absorber entropía negativa" para mantenerse en un estado altamente ordenado. Eso les permite actuar sobre el entorno. Para mantener constante o disminuir la entropía en su interior, los sistemas biológicos crean desorden en el ambiente. Algunos de estos sistemas, como los seres humanos, crean una cantidad de desorden muy superior a la que necesitan para perseverar en su ser, llegando incluso a destruir el medio ambiente y, así, amenazar su propia existencia. (Fig.5)
El metabolismo es el sistema de procesos que usa un organismo para transformar el alimento que toma del medio y disminuir su entropía. En la medida que un organismo es capaz de metabolizar alimentos se mantiene fuera del equilibrio termodinámico con el medio y puede actuar. Cuando pierde la capacidad de extraer orden del medio, rápidamente tiende "termalizar", y sucumbe. Decaer es aumentar la propia entropía, y morir llegar a su máximo valor posible respecto del entorno.
Ahora bien, la vida ha existido en la tierra por unos 4000 millones de años. ¿Porqué aún no se ha extinguido, llegando al equilibro térmico con el planeta a temperatura uniforme? La repuesta es que durante ese largo período la tierra no ha sido un planeta aislado, sino que ha estado disminuyendo su entropía a costa del medio en que se encuentra: el sistema solar y el sol mismo. El sol emite radiación electromagnética, en su mayoría con longitudes de onda correspondientes al ultravioleta y al rango visible del espectro. Esa radiación es recibida por la tierra, y re-emitida a una frecuencia mucho más baja, el infrarrojo. La energía de la tierra permanece constante en el proceso. Así, las cantidades de calor recibidas y entregadas son iguales, pero la temperatura que corresponde al infrarrojo es mucho más baja. De aquí que la radiación emitida por la tierra tiene una entropía mucho mayor que la recibida (recordemos que la temperatura entra dividiendo en la ecuación para el cambio de entropía). Luego, la tierra está permanentemente disminuyendo su entropía gracias al aumento de entropía del sol. La razón por la cual el sol brilla (sus reacciones termonucleares) en última instancia está relacionada con la fuerza gravitacional. La fuerza atractiva de la gravitación continúa haciendo trabajo en el sol porque originalmente la gravedad estaba muy lejos de un estado de equilibrio, o sea, de máxima entropía. Todos aquí en la tierra vivimos a costa de la baja entropía del campo gravitacional al comienzo del universo. (Fig.6)
- Caos, determinismo e irreversibilidad
La teoría del caos tiene su origen en los trabajos del matemático francés Herni Poincaré (1854-1912). Poincaré trabajó extensamente en dinámica, la rama de la física fundada por Newton y que estudia el comportamiento de sistemas físicos sometidos a fuerzas externas. El movimiento de un sistema dinámico se representa por medio de las funciones que describen su localización en cada instante del tiempo. Esas funciones se obtienen resolviendo ecuaciones diferenciales. La teoría de estas ecuaciones admite teoremas de existencia y unicidad de las soluciones. Esto es, conocidas las condiciones iniciales del problema y dadas las ecuaciones que tienen en cuenta las fuerzas involucradas, siempre existe una, y sólo una, solución. En ese sentido, se suele decir que la dinámica newtoniana es una ciencia determinista: planteado el problema, sabemos que dentro de la teoría existe una solución. Si el estado de un sistema en un cierto momento y lugar está determinado, entonces lo está toda su evolución ulterior. (Fig.7)
Lo que Poincaré encontró fue que existen sistemas dinámicos (llamados no-lineales) en los que una pequeña variación en las condiciones iniciales se ve reflejada en una inmensa variación de la trayectoria subsiguiente. Es posible probar la existencia de estos sistemas, precisamente, porque son deterministas y podemos estimar cuánto se apartan dos trayectorias originalmente muy próximas. En particular, si dos trayectorias originalmente están separadas por una distancia δ0 la separación evoluciona con el tiempo según la siguiente expresión:
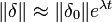
donde la doble barra representa el módulo del vector separación, t es el tiempo, y λ es una medida de la sensibilidad del sistema llamada exponente de Lyapunov. Si λ > O, las trayectorias divergen exponencialmente. Esto presenta un problema para la predictibilidad, ya que el error en las condiciones iniciales puede dar lugar a trayectorias completamente diferentes. Es muy importante remarcar, sin embargo, que esa falta de capacidad de predecir no implica una indeterminación, sino sólo una falta de conocimiento de las condiciones iniciales. Poincaré sintetizó esto diciendo que "El azar no es más que la medida de la ignorancia del hombre". Los sistemas dinámicos con comportamiento caótico, lejos de refutar el determinismo, lo confirman, al menos al nivel clásico. El determinismo implica dependencia de las condiciones iniciales y de los estados anteriores del sistema. Si no fuera válido, entonces no podríamos predecir que un sistema tendrá un comportamiento caótico. De hecho, no podríamos predecir la pérdida de predictibilidad que implica la gran susceptibilidad a las condiciones iniciales. (Fig.8)
Los sistemas caóticos son en general sistemas cuyo comportamiento se describe por medio de ecuaciones diferenciales hiperbólicas. Hay teoremas de existencia y unicidad para las soluciones de esas ecuaciones. De aquí que no pueda afirmarse que el caos implica indeterminación e irreversibilidad. De hecho, las ecuaciones del movimiento son perfectamente reversibles bajo inversión temporal. Nuestro conocimiento imperfecto del estado del mundo, sin embargo, nos imposibilita predecir el comportamiento detallado de sistemas caóticos, como la atmósfera, los océanos, y la dinámica de los sistemas biológicos y sociales.
Algunos autores, como el belga Ilya Prigogine (1917-2003), han sostenido que el caos es indeterminista, esencialmente irreversible, y que el concepto de trayectoria debería ser reemplazado por probabilidades. El problema con esta posición es que Prigogine considera que las probabilidades son "irreducibles". Esto es, considera a las probabilidades como básicas e imposibles de analizar en términos de trayectorias. Prigogine intenta, así, introducir una indeterminación ontológica en el mundo que describe la mecánica clásica. Esto es erróneo. Las probabilidades, si son usadas para estudiar sistemas dinámicos, se derivan de las propiedades de las trayectorias accesibles al sistema. El sistema, en todo momento, se encuentra en una posición o en otra, con una cierta velocidad. El sistema no es una nube de probabilidades de estar en tal o cual posición con tal o cual velocidad. Las probabilidades representan las faltas de nuestro conocimiento del sistema, no la indeterminación del sistema mismo. Afirmar que un sistema dinámico tiene una probabilidad p(x, t) de encontrarse en un lugar x en el instante t es como afirmar que el habitante medio de América tiene 2.3 hijos. Las personas reales no tiene hijos fraccionarios. El promedio es una forma de codificar nuestro conocimiento sobre un conjunto de eventos, y nuestra ignorancia sobre los eventos particulares. Más preocupantes aún, si cabe, son las especulaciones de Prigogine y colaboradores sobre el tiempo. (Fig.9)
- Tiempo y caos
Entre los muchos problemas asociados a la naturaleza del tiempo, uno de los más notables es la aparente direccionalidad con la que los diferentes eventos y procesos se desarrollan a medida que el tiempo "pasa". Envejecemos, pero nunca rejuvenecemos. Recordamos el pasado, pero apenas vislumbramos el futuro. Las cosas que fabricamos o compramos se rompen, descomponen, pero jamás se reparan solas. En definitiva, todos nos morimos, y eso es para siempre. El "devenir" es irreversible. Este tipo de situaciones han sido utilizadas para intentar relacionar tiempo con irreversibilidad, y con el caos. Se ha argumentado que los movimientos caóticos marcan una "dirección" preferencial para el transcurso del tiempo. En particular, D. Driebe, un colaborador de Prigogine, señala que "la flecha del tiempo no se debe a alguna aproximación fenomenológica sino que es una propiedad intrínseca de los sistemas dinámicos inestables". Como hemos mostrado antes, las leyes del caos son completamente reversibles bajo inversión temporal y no hay relación alguna entre caos y tiempo, más allá de ser éste un parámetro en las ecuaciones que describen los sistemas caóticos. El tiempo se representa por un parámetro de naturaleza escalar, no vectorial, por lo que no puede tener una dirección. Lo que puede tener dirección es un campo vectorial que señala, en cada punto del espacio y el tiempo, la dirección en que ocurren los procesos físicos. El que ése campo tenga una dirección depende de las condiciones iniciales de los procesos y de la topología global del espacio-tiempo, no de que los procesos sean caóticos (ver al respecto Romero & Pérez 2011). Recordemos que un sistema físico es llamado caótico si puede ser modelado por un conjunto de ecuaciones dinámicas que satisfagan las siguientes tres condiciones: son ecuaciones deterministas, las soluciones presentan recurrencia para tiempos grandes, y son altamente sensibles a cambios en las condiciones iniciales.
Nuestra ignorancia del futuro no debe ser confundida con una asimetría en el mundo físico. A los procesos que ocurren en el mundo no les incumbe que nuestro cerebro pueda registrarlos o no. Ocurren de acuerdo a patrones que solemos codificar en las "leyes físicas", usualmente representadas por ecuaciones diferenciales o diferencio-integrales. El comportamiento de los sistemas concretos sólo puede obtenerse resolviendo esas ecuaciones con condiciones iniciales y de contorno adecuadas. Es a través de esas condiciones que la irreversibilidad entra en el mundo, y que observamos una dirección privilegiada de ocurrencia de los procesos físicos (la llamada "flecha del tiempo").
- Caos cerebral
¿Porqué un científico de gran reputación como Prigogine se ha visto involucrado en elucubraciones tan poco científicas acerca del tiempo, la irreversibilidad y el caos? El punto de inflexión clave para Prigogine fue su encuentro con la filósofa belga Isabelle Stegners (nacida en 1949). En 1984 publicaron un libro conjunto, titulado La Nouvelle Alliance (La Nueva Alianza, titulado en inglés Order out of Chaos). Stengers introdujo a Prigogine en el estudio de intelectuales franceses como Gilles Deleuze (1925 - 1995) y otros escritores "postmodernistas", fuertemente influenciados por el psicoanálisis y que tienden a ver la ciencia como un mero "discurso" fruto del contexto social donde se realiza. Otros escritores de esta línea son Bruno Latour, Julia Kristeva, y Jean Baudrillard. Todos ellos suelen utilizar jerga científica, en especial proveniente de la física, en contextos sociales, dándole a los términos científicos un sentido cuanto menos confuso (para un crítica devastadora de estos intelectuales ver Sokal & Bricmont 1998). La aplicación de las ideas sobre termodinámica irreversible de Prigogine, junto con las concepciones sobre el tiempo tomadas por Stengers de otros pensadores, han dado lugar a un relato cosmológico que conforma uno de los más vastos sistemas de estupideces que ha formulado la mente humana.
En esta "cosmología" de Prigogine y Stegners el tiempo precede al Universo. Este último sería el resultado de una transición de fase a gran escala. El Universo se originaría en una inestabilidad sucedida a una situación que le ha precedido, sería el resultado de una transformación irreversible de otro estado físico: cuando el tiempo se transformó en materia. La ruptura de la simetría, en el espacio, es consecuencia de una ruptura en la simetría temporal, es decir, de una diferencia entre el pasado y el futuro. La materia lleva consigo el signo de la flecha del tiempo. Las estructuras disipativas rompen la simetría euclideana del espacio y la simetría del tiempo. Lejos del equilibrio, la materia adquiere nuevas propiedades...Es probable que el lector, perplejo, no pueda encontrar un sentido a todo esto. La razón es sencilla: no tiene sentido.
- La crisis cultural de occidente
Como acaso sucedió a muchos lectores, en mi juventud fui lector de Nietzsche. Nietzsche tiene muchos atractivos para la gente joven: escribió bien y sobre temas interesantes; lo hizo en forma fragmentaria, lo que congracia con la pereza inherente a cierta edad. Además, en la juventud la fuerza del cuerpo nos da certidumbres, soberbia, fatuidad. La "filosofía con el martillo" propugnada por Nietzsche se lleva muy bien con estas limitaciones. Sí, yo amé a Nietzsche, como tantos otros. Pero lo que más me atrajo de él no fue tanto su desprecio o sus doctrinas sobre el superhombre y el eterno retorno, sino la crítica de la cultura occidental que muchos de sus escritos permiten vislumbrar. Los años, el cansancio, los errores, me han ido alejando de su relectura; pero siempre mantengo fresca en mi memoria su crítica de la cultura occidental, y de ciertos tipos (casi podríamos llamar casos) culturales, entre otros el profesor universitario.
El siglo XX experimentó una crisis de valores que quizás no se había visto desde los fines de la antigüedad greco-latina. En la primera mitad del siglo se manifestó, entre otras cosas, en el irracionalismo defendido por escuelas filosóficas como el existencialismo y la fenomenología. En buena medida estos movimientos fueron herederos de ciertas reacciones románticas del siglo XIX al Iluminismo. En la segunda mitad del siglo XX, el desencanto de las juventudes universitarias con las formas clásicas de la academia, consecuencia, en parte, de la guerra de Vietnam y de los movimientos asociados al mayo francés de 1968, llevaron a un resurgimiento del irracionalismo y del relativismo. Esto acarreó, a su vez, un completo relajamiento de los estándares de rigor académico que hicieron posible la obra de autores como Paul Feyrabend en los Estados Unidos y de numerosos autores franceses como Foucault, Deleuze, Latour, y otros. Al principio este movimiento, llamado "posmodernista" y luego de "sociología de la ciencia", se caracterizó por su defensa del irracionalismo. Luego, fue mutando hacia la incorporación de jerga científica (pero no sus métodos) en pretendidos estudios sociales. El lector puede consultar Bunge (1999, 2001, 2012) para análisis extensos de estos temas.
Actualmente, y en especial luego del llamado "afaire Sokal" (ver Sokal & Bricmont 1998) estas tendencias están en retroceso en todo el mundo (con las posibles excepciones de Francia y Argentina). Sin embargo, la reacción de la academia ha sido negativa en el sentido de que la mayor parte de los trabajos que se publican actualmente en revistas filosóficas serias, apenas tienen que ver con la ciencia y en su gran mayoría se dedican a tratar minucias terminológicas o a discutir interpretaciones de otros autores. Si bien el viejo neopositivismo tenía fuertes limitaciones, al menos estaba inspirado por la investigación científica de su época. La actual crisis del pensamiento filosófico, que a veces también se hace sentir en ámbitos científicos, sólo será superada cuando se vuelva a tener el valor de abordar grandes temas con herramientas formales y en una forma informada por todas las áreas de la ciencia. La filosofía científica necesita de la ciencia, y la ciencia necesita una filosofía científica. La civilización occidental, me atrevo a escribir, necesita desesperadamente de ambas.
- Referencias y lecturas recomendadas
- Bunge, M. 1999, Social Science under Debate: A Philosophical Perspective, University of Toronto Press, Toronto.
- Bunge, M. 2001, Philosophy in Crisis: The Need for Reconstruction, Prometheus, Amherst, NY.
- Bunge, M. 2012, Evaluating Philosophies, Springer, Berlin.
- Dribe, D. 1994, Physics Today, Isuue: November, p.13.
- Penrose, R. 2002, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, University Press, Oxford.
- Prigogine, I. & Stengers, I. 1984, Order out of Chaos, Heinemann, London.
- Prigogine, I. & Stengers, I. 1988, Entre le Temp et l'Éternité, Fayard, Paris.
- Romero, G.E. & D. Pérez, D. 2011, "Time and irreversibility in an accelerating universe", Int. J. Modern Phys. D 20, 2831-2838.
- Schrödinger, E. 2012 (reprint), What is Life?: With Mind and Matter and Autobiographical Sketches, Cambridge University Press, Cambridge.
- Smith, L. 2007, Chaos: A Very Short Introduction, Oxford University Press, Oxford.
- Sokal, A. & Bricmont, J. 1998, Fashionable Nonsense: Postmodern Intellectuals' Abuse of Science, Picador, NY.
- Bunge, M. 2001, Philosophy in Crisis: The Need for Reconstruction, Prometheus, Amherst, NY.
- Bunge, M. 2012, Evaluating Philosophies, Springer, Berlin.
- Dribe, D. 1994, Physics Today, Isuue: November, p.13.
- Penrose, R. 2002, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, University Press, Oxford.
- Prigogine, I. & Stengers, I. 1984, Order out of Chaos, Heinemann, London.
- Prigogine, I. & Stengers, I. 1988, Entre le Temp et l'Éternité, Fayard, Paris.
- Romero, G.E. & D. Pérez, D. 2011, "Time and irreversibility in an accelerating universe", Int. J. Modern Phys. D 20, 2831-2838.
- Schrödinger, E. 2012 (reprint), What is Life?: With Mind and Matter and Autobiographical Sketches, Cambridge University Press, Cambridge.
- Smith, L. 2007, Chaos: A Very Short Introduction, Oxford University Press, Oxford.
- Sokal, A. & Bricmont, J. 1998, Fashionable Nonsense: Postmodern Intellectuals' Abuse of Science, Picador, NY.
- Sobre el autor
Gustavo E. Romero es Doctor en Física por la Universidad Nacional de La Plata. Actualmente es Profesor Titular de Astrofísica Relativista en la Facultad de Ciencias Astronómicas y Geofísicas de la UNLP e Investigador Principal del CONICET, con lugar de trabajo en el Instituto Argentino de Radioastronomía. Dirige el Grupo de Astrofísica Relativista y Radioastronomía (GARRA), ha sido Profesor Visitante de las universidades de Barcelona, Paris VII, Campinas y Hong Kong, entre otras, e Investigador Visitante del Max-Planck-Institut für Kernphysik (Heidelberg), el Service d'Astrophysique (Saclay, Francia), el Instituto di Astrofísica Spaziale e Física Cósmica (IASF, Bologna, Italia), etc.
Ha recibido los máximos premios a la investigación científica en Argentina: El Premio Bernardo Houssay del MinCyT (único argentino en recibirlo en dos oportunidades), el Premio J.L. Sérsic de la Asociación Argentina de Astronomía y el Premio E. Gaviola de la Academia Nacional de Ciencias. Fue Presidente de la Asociación Argentina de Astronomía. También ha recibido varias distinciones internacionales, incluyendo dos menciones de honor de la Gravity Research Foundation. El Dr. Romero ha publicado más de 300 artículos sobre gravitación, astrofísica, filosofía y religión. Entre sus libros se destacan "¿Es Posible Viajar en el Tiempo?" (Ed. Kaicron, BsAs, 2010) , "Introducción a la Astrofísica Relativista" (Publicaciones de la Universidad de Barcelona, 2011, junto a Josep M. Paredes), e "Introdution to Black Hole Astrophysics" (Springer, 2013, en colaboración con Gabriela S. Vila). Actualmente es Vice-director de nuestro Instituto.

