Figura 1: Modelo de máquina del tiempo imaginada por H.G. Wells, de acuerdo con la película de George Pal, The Time Machine (1960), protagonizada por Rod Taylor.
Figura 2: Albert Einstein en su despacho de Berlín, donde concibió la teoría general de la relatividad.
Figura 3: Karl Schwarzschild, en Potsdam.
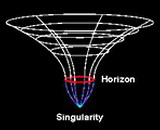
Figura 4: Esquema de un agujero negro de Schwarzschild. El objeto real tiene 4 dimensiones, una de las cuales ha sido removida para poder graficarlo.
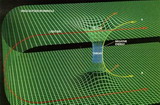
Figura 5: Diagrama de un agujero de gusano. A diferencia del agujero negro, no posee ni singularidad ni horizonte de eventos.
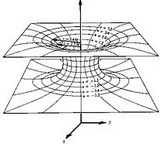
Figura 6: Un agujero de gusano conectando regiones distantes del espacio.
Figura 7: Agujero de gusano con materia exótica en su garganta, lo que produce repulsión gravitacional manteniendo el túnel abierto.
Figura 8: Agujero negro formado por materia normal colapsada a una singularidad
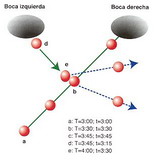
Figura 9: Agujero de gusano transformado en maquina del tiempo. Las bocas A y B se de-sincronizan.
Figura 10: Un agujero de gusano en New York
Figura 11: Bolas de billar y diferentes trayectorias posibles. Las que no son consistentes globalmente quedan descartadas por la conjetura de consistencia.
Figura 12: Fotograma de la serie El túnel del tiempo.
¿Es posible viajar en el tiempo?
- Introducción
En 1895, al comienzo de su carrera como novelista, el periodista y sociólogo inglés Herbert George Wells (1866-1946) publicó la novela The Time Machine, que se transformaría en texto un clásico y precursor de la literatura de ciencia ficción. En la novela, el protagonista, the time traveller, expresaba: [El hombre civilizado] puede vencer la gravedad utilizando globos, ¿por qué no le sería entonces posible también detener o acelerar su fluir por la dimensión temporal, o incluso revertirlo y viajar hacia atrás en ella?. Cien años después de la aparición de The Time Machine la humanidad ha vencido la gravedad no sólo mediante globos sino con máquinas que pesan cientos de toneladas. Aviones que alcanzan velocidades supersónicas, satélites artificiales que orbitan la Tierra, sondas espaciales que exploran la superficie de otros planetas y llegan hasta los confines del sistema solar, constituyen ejemplos adicionales del dominio de la naturaleza adquirido desde la época de Wells. ¿Pero qué ha sucedido con la dimensión temporal? ¿Admiten las leyes de la física, tal como se conocen en el presente, la posibilidad de construir máquinas del tiempo?
La teoría que en principio permite esbozar una respuesta a la pregunta de Wells es la Relatividad General, que fue enunciada por Albert Einstein apenas 20 años después de la publicación de la primera edición de The Time Machine. Einstein postuló, en contra de lo pensado hasta entonces, que la estructura geométrica del espacio y del tiempo no es absoluta sino que está determinada por la distribución de masa y energía existente en el Universo. Esto significa que la distancia entre dos puntos del espacio-tiempo es alterada por la presencia de cuerpos masivos o energéticos. ¿Pero puede dicha alteración ser suficiente como para que al recorrer una pequeña distancia en un tiempo corto de acuerdo con nuestro reloj podamos alcanzar puntos que están muy alejados, tanto en el espacio como en el tiempo, para otros observadores? ¿Puede suceder que, acaso, el tiempo se distorsione al punto de que podamos alcanzar nuestro pasado?
Responder a estas preguntas implica entender la naturaleza misma del espacio y el tiempo. Estas preguntas están relacionadas con otras, de tipo filosófico, como ¿Qué son el espacio y el tiempo? ¿Existe el pasado? ¿Existe el futuro? ¿Si el pasado y el futuro existen, son modificables desde el presente? ¿Somos libres o nuestras acciones están determinadas?
En la teoría Newtoniana del espacio y el tiempo, el primero es como un escenario vacío en el que ocurren los eventos, y el segundo es como un fluido, constante, que recorre todo el espacio permitiendo el cambio. Aunque podemos formular una teoría Newtoniana de la gravitación en un lenguaje de 4 dimensiones, tres espaciales y 1 temporal, no podemos dentro de esa teoría desplazarnos por la dimensión temporal como podemos hacerlo por las dimensiones espaciales. Nos movemos en las dimensiones espaciales respecto de la dimensión temporal. Esto es, para ir de la posición A a la B debemos adquirir una velocidad V que debe ser diferente de cero respecto de A. Si queremos movernos en el tiempo, esto es, ir del instante t1 al instante t2, deberíamos adquirir velocidad respecto a una quinta dimensión, un "super-tiempo". Así, por ejemplo, nos moveríamos a 12 segundos por segundo, donde el primero "segundo" pertenece al tiempo y el segundo "segundo" al "super-tiempo". No hay evidencia alguna de que tal "super-tiempo" exista. De hecho, aunque existiese, una maquina del tiempo como la que imaginó H.G. Wells (ver figura 1), jamás podría funcionar.
La razón es muy sencilla. La máquina posee una palanca: si se mueve hacia delante, avanza hacia el futuro, si se mueve hacia atrás, retrocede al pasado. La máquina siempre permanece en el mismo lugar del espacio. Es obvio que al no moverse la máquina, en los instantes anteriores y posteriores al accionarse de la palanca, el lugar ocupado por la máquina estará ocupado por la propia máquina, que entonces colisionará con ella misma. Esto nos muestra, que si el viaje en el tiempo es posible, debe implicar siempre un viaje en el espacio también.
Los elementos para poder pensar seriamente en la posibilidad física del viaje en el tiempo sólo comenzaron a aparecer con la formulación de la teoría general de la relatividad por Albert Einstein (1879-1955, Fig.2), en noviembre de 1915. Las ecuaciones de Einstein relacionan la geometría (en palabras técnicas, la métrica, o sea la forma en la cual se miden las distancias) del espacio-tiempo con el contenido de energía e impulso de los sistemas físicos que lo forman. El espacio-tiempo fue introducido en 1907 por el matemático Herman Minkowski (1864-1909) y puede definirse con el conjunto de todos los eventos que suceden a todas las cosas. Un evento es un cambio en el estado de una cosa. O sea, que todo lo que ha sucedido, sucede, o sucederá son elementos, o puntos, del espacio-tiempo. Einstein mostró que la geometría de ese conjunto está determinada por la ontología, esto es, el tipo de cosas que existen. Sus ecuaciones permiten calcular la métrica, y por tanto la forma de medir las distancias en el espacio-tiempo, si se conoce la cantidad de la energía y el impulso de las cosas concretas.
El astrofísico alemán Karl Schwarzschild (1873-1916, Fig. 3) halló la primera solución exacta a las ecuaciones de Einstein en 1916. Schwarzschild, que por ese entonces servía en el ejército alemán combatiendo en el frente ruso, tomó conocimiento de las ecuaciones de Einstein en diciembre de 1915, a través de un número de los Anales de la Academia Prusiana de Ciencias que contenía la comunicación original de Einstein. En poco tiempo desarrolló una solución para estas ecuaciones que envió al propio Einstein quién, en enero de 1916, la comunicó a la Academia en nombre de Schwarzschild. Cuatro meses más tarde Schwarzschild murió, sin conocer la riqueza del sistema físico descripto por la solución que ahora lleva su nombre. La solución de Schwarzschild define la curvatura del espacio-tiempo en las proximidades de un cuerpo masivo y compacto como, por ejemplo, una estrella. Esta solución permitió calcular cuánto se desviarían de la trayectoria rectilínea los rayos de luz provenientes de estrellas lejanas al pasar cerca del sol como consecuencia de la curvatura que este causa en el espacio-tiempo que lo circunda. En 1919, una expedición a la Isla del Príncipe en África Occidental, dirigida por Arthur S. Eddington (1882-1944), proporcionó la primera verificación de la solución de Schwarzschild a las ecuaciones de Einstein. Durante un eclipse total de sol, Eddington y sus colaboradores, realizaron mediciones que mostraron que las posiciones de las estrellas inmediatamente vecinas al disco solar aparecían desplazadas respecto de la posición que mostraban en ausencia del astro.
La solución de Schwarzschild, además de predecir el comportamiento de la luz y otras partículas en las cercanías de una estrella, incluye otras predicciones que inicialmente pasaron casi desapercibidas. Entre ellas cabe señalar aquella que indica que, si el radio de la estrella es menor que un cierto valor crítico dependiente de su masa (conocido hoy como radio de Schwarzschild), la distorsión del espacio-tiempo sería tal que la estrella quedaría "separada" del universo por un "horizonte". Ningún objeto proveniente de la estrella podría jamás cruzar este horizonte y alcanzar el "exterior". La estrella se habría transformado en un cuerpo completamente negro, un agujero en el cual sólo pueden caer objetos (partículas, luz, objetos) pero de donde nada puede escapar jamás.
Estos objetos, denominados a partir de los años 1960 como agujeros negros, son algo así como un precipicio en el espacio-tiempo. En su interior reside una región pequeña, conocida como la singularidad, que constituye el destino final de todo lo que cae en ellos. Alli, incluso las ecuaciones de Einstein dejan de ser válidas. En la Fig. 4 mostramos el esquema de un agujero negro.
La mayoría de los físicos de la época, incluyendo a Einstein, adoptaron una actitud escéptica; y no creyeron que objetos como los agujeros negros pudieran existir en el universo real. Sin embargo, en 1939, los físicos norteamericanos J. Oppenheimer (1904-1967, quien años más tarde lideraría los esfuerzos estadounidenses para producir la bomba atómica) y Hartland Snyder (1913-1962, en ese momento un estudiante de postgrado) demostraron por medio de cálculos detallados que cuando su combustible nuclear se agota, cualquier estrella cuya masa sea al menos tres veces mayor que la del sol termina por colapsar bajo la acción de la fuerza gravitatoria que ella misma genera. Los cálculos de Oppenheimer y Snyder indicaban que el colapso no se detiene (como sostenían los detractores de la idea de agujero negro), sino que continúa hasta que el radio de la estrella se hace inferior al radio crítico y se forma un agujero en el propio espacio-tiempo.
Aún después de la publicación de los hallazgos de Oppenheimer y Snyder, la existencia de los agujeros negros siguió siendo negada por la mayoría de los físicos, principalmente porque la solución de Oppenheimer y Snyder presentaba características que en ese momento fueron catalogadas como "no físicas", entre las que sobresalía el hecho de que para dos valores específicos de una de las coordenadas, ciertas funciones asociadas con la distancia entre dos puntos del espacio-tiempo se hacían divergentes.
La oposición a la existencia de agujeros negros fue liderada durante algún tiempo por uno de los más grandes científicos de este siglo: John Archibald Wheeler (1911-2008, quien durante los años 50 dirigió el desarrollo de la bomba de hidrógeno en EEUU). Wheeler sostenía que los cálculos de Oppenheimer y Snyder contenían demasiadas idealizaciones (es decir simplificaciones de los datos a fin de disponer de un modelo susceptible a su tratamiento matemático). Wheeler, sin embargo, cambió su posición y retiró sus objeciones cuando al rehacer los cálculos de Oppenheimer y Snyder, teniendo en cuenta correcciones provenientes de la física nuclear, logró probar hacia 1958 que estos autores tenían razón al postular que la formación de un agujero era inevitable. Desde entonces Wheeler se transformó en uno de los líderes en la investigación de objetos colapsados por acción de la gravedad.
Sin embargo, subsistían aún las dudas acerca de la existencia de los agujeros negros debido a las divergencias en la geometría del espacio-tiempo que aparecían en el horizonte de eventos. Los científicos se preguntaban si era esta una característica fundamental del espacio-tiempo de Schwarzschild o más bien era la consecuencia de la incorrecta elección de las coordenadas utilizadas para describirlo. También generaba dudas el hecho que la solución predice la existencia de un punto de curvatura infinita (vale decir, un punto en el cual la fuerza gravitatoria es infinita, y el espacio-tiempo deja de existir de acuerdo con la relatividad general), la ya mencionada singularidad central.
En 1960, Martin Kruskal (1925-2006) y otros, revisaron el asunto utilizando un nuevo sistema de coordenadas, que incluye al anterior, mediante un procedimiento matemático llamado extensión analítica. Lograron demostrar que la solución de Schwarzschild no representa a un único universo sino a dos: uno es el principal o primario, digamos, donde residimos nosotros, y otro, inaccesible, es el secundario, separado del primero por la existencia de la singularidad y aislado del mismo por el horizonte de eventos. La ubicación del horizonte y las propiedades del mismo no habían sido estudiadas durante las primeras etapas del desarrollo de la relatividad general, debido a que el valor de la coordenada radial a la cual aparece el horizonte se encuentra siempre dentro de los cuerpos (en donde la solución de Schwarzschild no es válida) cuando estos no son suficientemente compactos. Por ejemplo, para una estrella como el sol, el radio de Schwarzschild se ubica a 3 kilómetros del centro, mientras que el radio solar es de varios miles de kilómetros.
Solamente cuando los físicos consideraron seriamente la existencia de objetos superdensos, los estudios de la solución de Schwarzschild en este rango de distancias cobraron importancia. Utilizando las coordenadas de Kruskal resultó posible demostrar que ningún objeto que se desplace a velocidades menores que la de la luz puede evitar caer en la singularidad antes de alcanzar el universo secundario. Aunque existe un "puente" conectando ambos universos (llamado puente de Einstein-Rosen) el problema es que este evoluciona con el tiempo de modo tal que se cierra sobre sí mismo antes que cualquier objeto pueda atravesarlo. A pesar de ello, el descubrimiento de estas nuevas propiedades de la solución de Schwarzschild despertó el interés en el estudio de estructuras topológicas (es decir, de forma) que presenten puentes o túneles que puedan ser atravesables para unir así distintas regiones del espacio-tiempo.
Esta idea fue retomada hacia fines de los años 1980 por Kip Thorne (1940 - ), titular de la cátedra Feynman en el Instituto Tecnológico de California, cuando fue consultado por Carl Sagan, que se encontraba entonces escribiendo su novela Contact sobre la posibilidad de utilizar agujeros negros para realizar viajes interestelares. La consulta provocó el interés de Thorne por el tema, quien luego de trabajar un tiempo sobre el asunto, explicó a Sagan que los agujeros negros de Schwarzschild no son "atravesables" a causa de la presencia de la singularidad y del horizonte de eventos descritos arriba. En la opinión de Thorne, la estructura que Sagan estaba buscando para fundamentar el argumento de su novela era aquella solución de las ecuaciones de Relatividad General que actualmente se conoce como agujero de gusano, y que puede imaginarse como un túnel que une regiones no contiguas del espacio-tiempo (Figura 5).
Thorne, junto con sus alumnos Mike Morris y Ulvi Yurtsever, se dedicó entonces al estudio de las características que debería tener la materia que constituye el túnel, para poder distorsionar el espacio-tiempo de manera tal que la conexión resultante fuese permanente y atravesable. Utilizando las ecuaciones de Einstein, lograron probar que el túnel sólo podría mantenerse abierto si sus paredes fueran de materia exótica, esto es materia que a diferencia de normal debe poseer masa negativa (en el argot técnico, su tensión radial debe ser mayor que su densidad de energía). Este material se dice que viola las condiciones de energía, esto es, ejerce repulsión gravitatoria.
La existencia de cantidades macroscópicas de materia exótica haría más probable la presencia de agujeros de gusano en algún lugar del universo. Tales objetos podrían utilizarse para viajar a regiones distantes en tiempos menores de los que se necesitarían si el viaje se hiciese por el espacio "convencional". La Figura 6 muestra cómo un agujero de gusano podría usarse como un atajo para unir puntos distantes en el universo. En este tipo de diagramas, el universo se representa como una lámina de dos dimensiones en la que el agujero de gusano puede unir puntos distantes porque la lámina está plegada en el espacio externo.
La materia exótica debe estar ubicada en la "garganta" del agujero de gusano, para que esta no se cierre bajo la atracción gravitatoria produciendo una singularidad y un agujero negro. Esto se ilustra en la Fig. 7. Para comparación en la Fig. 8 mostramos un agujero negro.
- Viajes a través del tiempo
Dejemos ahora de lado los viajes por el espacio y examinemos con algún detalle las posibilidades de viajar hacia el futuro o el pasado. Desde el punto de vista de la teoría de la relatividad especial, es factible viajar hacia el futuro utilizando el fenómeno de dilatación temporal que esta teoría predice. Para discutir este fenómeno con un poco más de detalle imaginemos que existen dos observadores, o mejor, dos sistemas de referencia inerciales. En el sistema asociado con una dada partícula, el intervalo espacio-temporal entre dos eventos coincide con el lapso de tiempo medido por un reloj. Dicho intervalo se llama tiempo propio. A través de la ecuación que define la distancia entre dos eventos la relatividad especial nos muestra que el tiempo medido en la coordenada propia es siempre menor que el tiempo medido por el observador no acelerado.
La dilatación temporal ha sido confirmada de muchas maneras, por ejemplo, observando la propagación de partículas sub-atómicas que generalmente viajan a velocidades cercanas a la de la luz. Esto se conoce desde la década de 1910, cuando en una serie de vuelos en globo, Victor Hess (1883-1964) descubrió que la Tierra se encuentra inmersa en un mar de radiación cósmica. Hoy se sabe que esta radiación esta formada mayoritariamente por muones creados por la interacción de los rayos cósmicos con los átomos presentes en la alta atmósfera. Los muones viajan varios kilómetros antes de impactar en la superficie terrestre. Sin embargo, en su sistema de referencia propio sólo viven alrededor de dos microsegundos, tiempo en el cual podrían recorrer no más que algunos cientos de metros. La explicación de cómo es que los muones llegan a la superficie del planeta es la dilatación del tiempo predicha por la relatividad especial: como consecuencia de la misma el tiempo de vida de los muones aumenta cuando es medido desde nuestro sistema de referencia.
Este efecto de dilatación temporal podría utilizarse para facilitar el viaje de seres humanos hacia el futuro. El viajero del tiempo debería ser también un viajero espacial, cuya nave se debería mover a una fracción significativa de la velocidad de la luz (que es de unos 300.000 km/s en el vacío). Cuando le viajero volviese a la Tierra, luego de un viaje de algunos años, dependiendo de su velocidad, podría llegar cientos o miles de años luego de su partida. Sin embargo, no habría forma para él de volver a su tiempo. La relatividad especial sólo permite viajar el futuro. El pasado permanece inalcanzable.
Pocos años después de que Einstein formulara su teoría, se encontraron las primeras soluciones que describen regiones de espacio-tiempo con curvas temporales cerradas, esto es, curvas según las cuales na partícula que se mueve siempre en dirección de su futuro local termina arribando a algún punto de su propio pasado. Entre estas soluciones se destacan el cilindro de longitud infinita y compuesto de polvo en rotación rápida de Willem Jacob van Stockum (1910-1944), y el Universo en rotación propuesto por Kurt Gödel (1906-1978). La matemática de estas soluciones muestra que ambas contienen trayectorias en el espacio-tiempo que permiten viajar hacia el pasado y retornar al presente. Sin embargo, estos modelos han sido catalogados como carentes de significado físico por la mayor parte de la comunidad científica dado que no existen cilindros infinitos, y se sabe que el Universo no rota.
Más recientemente, a mediados de la década 1970, Frank Tipler (1947 - ) demostró que la construcción de una máquina del tiempo de tamaño finito que satisfaga las ecuaciones de Einstein requiere un material que viole las condiciones de energía. Esta demostración es motivo suficiente para justificar que las expectativas de construir en el futuro una máquina del tiempo se concentren en los agujero de gusano.
Es relativamente simple visualizar cómo la presencia de agujeros de gusano atravesables permitiría construir máquinas del tiempo. La idea fundamental de este mecanismo fue propuesto por Morris, Thorne y Yurtserver, y se basa en la combinación de algunos conceptos de Relatividad Especial con la estructura de un agujero de gusano atravesable. Supongamos un agujero de gusano con dos bocas, A y B, como se muestra en la Figura 9. Ambas bocas conectan regiones separadas en el espacio y sincronizadas en el tiempo, esto es, un reloj en la boca A marca la misma hora que un reloj en la boca B.
Supongamos ahora que la distancia desde A hasta B puede ser recorrida, digamos, en 1 hora. Así, si alguien entra por la boca A a las 12 hs, sale por la boca B a las 12 hs y luego demora en llegar a la boca A 1 hora, esto es, arriba a las 13 hs. Imaginemos que podemos de-sincronizar los relojes, por ejemplo moviendo una de las bocas a velocidad relativista o exponiéndola a un campo gravitacional intenso. El resultado de esta de-sincronización será que cuando en una boca (la A) sean las 12 hs, en la boca B sean las 10 hs. Así, un viajero puede entrar a la boca A a las 12 hs, salir por la B a las 10 hs, viajar hacia la boca A demorando una hora, y llegar allí a las 11 hs. No tiene más que sentarse a esperar una hora para verse a si mismo llegar a las 12 hs para iniciar el viaje. Nuestro viajero es un viajero del tiempo que ha llegado a su propio pasado.
Un espacio-tiempo donde son posibles maquinas del tiempo es un espacio-tiempo del cual se dice tiene violación cronológica. Si sólo una parte del espacio tiempo admite la posibilidad de curvas temporales cerradas como la descripta más arriba, la superficie que separa de región con violación cronológica de la región donde ésta no es posible se llama horizonte cronológico. Existen varios problemas asociados a la estabilidad del horizonte cronológico. Cabe mencionar en especial, el efecto del crecimiento de las fluctuaciones de vacío de campos cuánticos que podría producirse si éstas atravesaran repetidas veces el túnel. La posibilidad de que este efecto sea suficiente para evitar que pueda construirse una máquina del tiempo será probablemente respondido por la aún inexistente teoría cuántica de la gravitación. Sin embargo, no hay nada en la teoría de la relatividad general que parezca impedir la existencia de de regiones de violación cronológica si se puede generar una cantidad macroscópica suficiente de materia exótica (hace falta aproximadamente 1 masa solar de esta materia para mantener abierta la garganta de un agujero de gusano de unos metros de diámetro).
¿Cuál es el aspecto de la boca de un agujero de gusano visto por un observador externo? La geometría más sencilla para un agujero de gusano es la esférica. En tal caso, lo que vería un observador sería una especie de esfera de la cual saldría luz originada en eventos próximos a la otra boca. Si esa boca está en un lugar distante, lo que se vería sería el paisaje de ese lugar. En la Figura 10 se muestra una ilustración donde una boca del agujero de gusano aparece en Time's Square, New York City.
- Supuestas paradojas generadas por los viajes en el tiempo
El viaje en el tiempo plantea una serie de interesantes paradojas que pueden agruparse básicamente en dos tipos.
- Paradojas de consistencia: Se trata de aquellas del tipo "el viajero mata a su madre antes de que él mismo nazca". Este tipo de paradojas suceden si el viajero puede actuar sobre el pasado cambiándolo.
- Paradojas de creación a partir de la nada: En este caso, un viajero vuelve al pasado con, por ejemplo, la versión final de este artículo y la entrega al autor antes de que sea escrito. Luego, el autor, en el pasado, no necesita escribir el artículo, ya que posee la versión final. Pero alguien tuvo que haber escrito el artículo, y si no el autor, ¿quién, entonces, escribió este artículo? Esta tipo de paradojas se puede dar con objetos físicos. Supongamos que el viajero lleva un reloj al pasado. Se encuentra consigo mismo, y se regala el reloj. Lleva el reloj en su muñeca hasta que realiza el viaje en el tiempo y se regala el reloj. ¿De dónde salió el reloj?
Las paradojas, o bien son aparentes y por tanto pueden disolverse por medio de un análisis más profundo o por medio de hipótesis suplementarias, o bien implican una contradicción, que hace que las hipótesis iniciales deban rechazarse (en este caso la posibilidad del viaje en el tiempo).
Si bien las ecuaciones de Einstein admiten soluciones donde el viaje en el tiempo es posible, podría suceder que éste nunca se dé porque entra en contradicción con otras leyes de la física. Por ejemplo, podría ser que el viaje en el tiempo podría violar el principio de causalidad, como parecen sugerir las paradojas. Sin embargo, este problema se resuelve adoptando una hipótesis adicional muy sencilla, la conjetura de consistencia, que puede formularse de la siguiente forma:
Conjetura de consistencia: la historia del universo es única, y no es posible modificar lo que ya ha sucedido.
Expresado en forma más técnica: las únicas soluciones a las ecuaciones que expresan las leyes de la física que pueden describir hechos que suceden localmente en el universo son aquellas que son consistentes en forma global (toda acción que se realice aquí y ahora debe ser consistente con la historia global del universo; si el viajero temporal fuera a matar a su madre en un instante previo a su nacimiento, esta conjetura demanda que el intento fracase). Se ha argumentado que la conjetura de consistencia se vuelve poco probable si los intentos por cambiar el pasado se repiten. Por ejemplo, una vez el potencial matricida puede tropezar antes de disparar sobre su no muy querida madre, otra vez la pistola puede fallar, otra la madre se puede agachar en el momento justo, etc. La probabilidad acumulada de todos estos eventos independientes es bajísima. Sin embargo, este razonamiento es incorrecto. La probabilidad de fallar es siempre uno. Lo mismo sucede con las maquinas de movimiento perpetuo: no importa lo que haga el constructor, siempre fallará, ya que las leyes mismas de la física prohíben la posibilidad de una máquina de movimiento perpetuo. La forma en que fallará el constructor, depende de la forma en que trate de perpetrar la construcción de su máquina. Lo mismo sucede con los intentos de cambiar el pasado. Sea lo que sea que hagamos en el pasado, ya lo hicimos, y nada va a cambiar.
Se ha argumentado también, en un famoso artículo de Stephen Hawking, que si bien la existencia de agujeros de gusano atravesables está permitida por las leyes de la física, los viajes en el tiempo no son posibles; efectos cuánticos impedirían construir una máquina del tiempo. Para elaborar esta conjetura, Hawking se apoyó en la observación de que no hay evidencia alguna de turistas del futuro. Esta afirmación fue objetada por Thorne, quien probó que: (1) las máquinas del tiempo no permiten viajes a tiempos anteriores al de su creación, y (2) hasta el día de hoy, ninguna máquina del tiempo ha sido construida.
Para cuantificar el problema, es posible reformular la paradoja del matricidio en términos mecánicos, lo que da como resultado la llamada crisis de las bolas de billar. Esto evita la discusión del estatus del libre albedrío frente a la existencia de CTCs. Como se muestra en la Fig. 11, imaginemos que una bola de billar, luego de entrar por la boca derecha de un agujero de gusano --convertido en una máquina del tiempo por el procedimiento descripto antes-- atraviesa el túnel en dirección de impacto consigo misma antes de que haya ingresado al agujero de gusano, impidiéndole la entrada al mismo. Las leyes de la mecánica clásica determinan una única trayectoria posible para cada conjunto de condiciones iniciales. Por el contrario, el estudio llevado a cabo por los alumnos de Thorne, Fernando Echeverria y Gunnar Klinkhammer, demostró que la existencia de máquinas del tiempo hace posible un número infinito de trayectorias para el movimiento de la bola. De ellas, sólo algunas son consistentes en sentido global, y es de esperar que éstas sean las que ocurran en el universo real.
¿Qué podemos decir de las paradojas de creación a partir de la nada? En el caso de objetos "auto-existentes", para que puedan satisfacer la conjetura de consistencia, el estado de los mismos no debe variar a lo largo de la trayectoria por la CTC. Si el objeto es macroscópico, su entropía cambiará, por lo que no podría existir. Sin embargo, objetos simples como partículas elementales, podrían existir en CTCs, ya que para ellos no se puede definir la entropía. También un objeto macroscópico, sobre el cual se realice trabajo que compense exactamente los cambios entrópicos podría habitar una CTC. Se ha llegado a sugerir, incluso que el universo mismo podría ser un objeto auto-existente en este sentido.
Si bien la conjetura de consistencia parece excluir a buena parte de la ontología bizarra objetos auto-existentes, nada impide que exista información autogenerada, como en el ejemplo del artículo mencionado antes. Esta información sería una especie de característica misma del espacio-tiempo.
Es importante destacar que el viaje en el tiempo no implica una violación de la causalidad. Más bien, implica que la causalidad en sentido global puede actuar desde el futuro hacia el pasado, pero localmente, siempre opera desde el pasado hacia el futuro.
Sin duda la mera posibilidad del viaje en el tiempo plantea fascinantes problemas filosóficos relacionados con la existencia del pasado y del futuro, el libre albedrío, y otros temas que han sido fuente de perplejidad para los filósofos durante más de 2 milenios. Recién a partir de principios del siglo XX estos temas pueden ser tratados con los métodos propios de la ciencia.
- Glosario:
- Curva temporal cerrada (CTC): trayectoria en la cual un observador que parte de un punto dado del espacio-tiempo y viajando siempre hacia el futuro (indicado por el cono de luz local) vuelve, al cabo de un cierto lapso, al punto de partida.
- Fluctuaciones de vacío: oscilaciones en los valores de los campos (por ejemplo, electromagnéticos o gravitatorios) debido a intercambios momentáneos de energía entre regiones adyacentes del espacio-tiempo.
- Horizonte de eventos: superficie del espacio-tiempo que delimita una región (interior) de la cual nada puede escapar. Las propiedades del horizonte son semejantes a las de una membrana que sólo deja pasar sustancias en una dirección.
- Horizonte cronológico: superficie que divide al espacio-tiempo en dos regiones, una donde la formación de CTCs es posible y otra donde éstas no existen.
- Principio de la relatividad: las leyes de la física no deben ser capaces de distinguir un sistema de referencia inercial de otro, esto es, deben tomar la misma forma en todos los sistemas.
- Relatividad general: teoría formulada por Einstein, que describe la dinámica del campo gravitacional.
- Singularidad: región de espacio-tiempo donde la curvatura se hace tan fuerte que las leyes de la relatividad general no son más válidas y debería describirse por una teoría cuántica de gravitación. Si se extrapolara la relatividad general a este dominio, se encontraría que las fuerzas gravitatoria son infinitas.
- Sistema de referencia inercial: un laboratorio idealizado para realizar experimentos, que se mueve a través del espacio sin aceleración.
- Lecturas sugeridas
- L.A. Anchordoqui, D.F. Torres, G.E. Romero & S.E. Perez Bergliaffa, Túneles en el espacio y el tiempo, Ciencia Hoy 55, 38-49, 2000.
- J.R. Gott, Time Travel in Einstein's Universe: the Physical Possibilities of Travel through Time (Houghton Mifflin Company, Boston, 2001).
- P. Nahin, Time Machines (AIP, New York, 1993).
- G.E. Romero, & D.F. Torres, Self-existing objects and auto-generated information in chronology-violating space-times: A philosophical discussion, Modern Physics Letters A 16, 1213-1222, 2001.
- G.E. Romero, God, causality and the creation of the Universe, Invenio 13, 11-20, 2004.
- K. S. Thorne, Black Holes and Time Warps: Einstein's Outreageous Legacy (W.W. Norton & Co., New York, 1994).
- D. F. Torres, G. E. Romero & L. A. Anchordoqui, Wormholes, gamma ray bursts and the amount of negative mass in the universe, Modern Physics Letters A13, 1575 (1998) (Honorable Mention, Gravity Research Foundation Awards 1998).
- M. Visser, Lorentzian Wormholes (AIP, New York, 1996).
- Sobre el autor:
Gustavo E. Romero es Doctor en Física por la Universidad Nacional de La Plata. Actualmente es Profesor de Astrofísica Relativista en el Facultad de Ciencias Astronómicas y Geofísicas de la UNLP e Investigador Principal del CONICET, con lugar de trabajo en el Instituto Argentino de Radioastronomía. Dirige el Grupo de Astrofísica Relativista y Radio Astronomía (GARRA), ha sido Profesor Visitante de las universidades de Barcelona, Paris VII, Campinas y Hongk Kong, entre otras, e Investigador Visitante del Max-Planck-Institut für Kernphysik (Heidelberg), el Service d'Astrophysique (Saclay, Francia), el Instituto di Astrofísica Spaziale e Física Cósmica (IASF, Bologna, Italia), etc. Ha recibido los máximos premios a la investigación científica en Argentina: El Premio Bernardo Houssay del MCyT, y el Premio E. Gaviola de la Academia Nacional de Ciencias. Actualmente es Presidente de la Asociación Argentina de Astronomía.